本文是本科毕业论文系列的第三篇,其他各篇请见《本科毕设:交流伺服系统控制环路问题研究》
本文将具体介绍永磁同步电机控制过程中的完全解耦策略。
根据上文《永磁同步伺服的闭环控制方法》,我们得到电流方程
(1) ![Rendered by QuickLaTeX.com \begin{align*} I_d(s)&=\frac{1/R_1}{1+(L_d/R_1)s}\left[U_d(s)+L_qI_q(s)\omega_r(s)\right] \\ I_q(s)&=\frac{1/R_1}{1+(L_q/R_1)s}\left[U_q(s)-L_dI_d(s)\omega_r(s)-\Psi_f\omega_r(s)\right] \label{eq:Iq} \end{align*}](https://stringblog.com/wp-content/ql-cache/quicklatex.com-e5a68e83913bbf8c10acffbc761ca6e1_l3.png)
(2) ![]()
为了使永磁同步电机获得更好的控制性能,往往需要对系统进行完全解耦。现考虑式(1)中的扰动分量,此时![]() 、
、![]() 轴电流耦合情况如图1所示。
轴电流耦合情况如图1所示。

图1 ![]() 、
、![]() 轴电流耦合示意图
轴电流耦合示意图
图1中,逆变器模型仍为式(2);电机模型仍为式(1),不再进行简化。此时有如下的传函关系
(3) ![Rendered by QuickLaTeX.com \begin{align*} I_d(s)&=\frac{1/R_1}{1+(L_d/R_1)s}\left[\frac{K_V}{T_Vs+1}U_{cd}(s)+pL_qI_q(s)\omega_m(s)\right] \\ I_q(s)&=\frac{1/R_1}{1+(L_q/R_1)s}\left[\frac{K_V}{T_Vs+1}U_{cq}(s)-pL_dI_d(s)\omega_m(s)-K_e\omega_m(s)\right] \label{eq:Iq2} \end{align*}](https://stringblog.com/wp-content/ql-cache/quicklatex.com-0308ca19e6513c617557fdd3d088e045_l3.png)
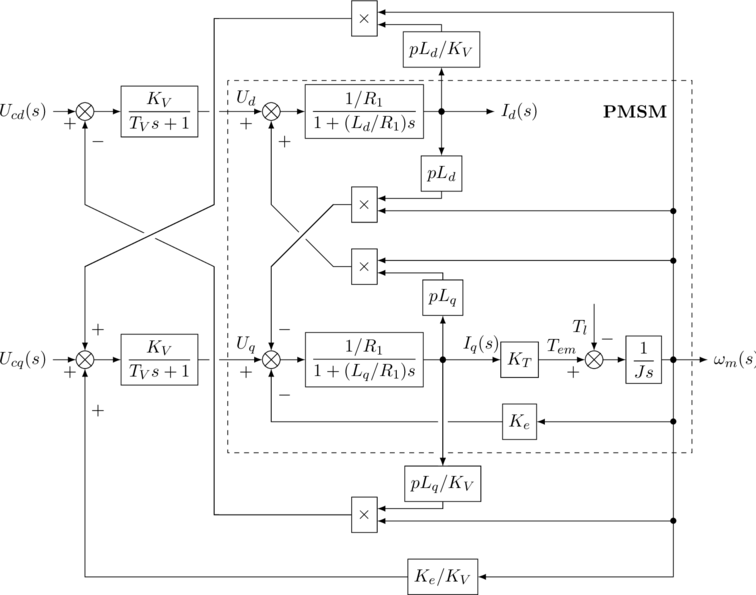
图2 ![]() 、
、![]() 轴电流解耦示意图
轴电流解耦示意图
(4) ![Rendered by QuickLaTeX.com \begin{align*} I_d(s)&=\frac{1/R_1}{1+(L_d/R_1)s}\left[\frac{K_V}{T_Vs+1}\right.\\ &\left.\times\left(U_{cd}(s)-\frac{pL_q}{K_V}I_q(s)\omega_m(s)\right)+pL_qI_q(s)\omega_m(s)\right]\notag\\ I_q(s)&=\frac{1/R_1}{1+(L_q/R_1)s}\left[\frac{K_V}{T_Vs+1}\right.\label{eq:Iq3}\\ &\left.\times\left(U_{cq}(s)+\frac{pL_d}{K_V}I_d(s)\omega_m(s)+\frac{K_e}{K_V}\omega_m(s)\right)-pL_dI_d(s)\omega_m(s)-K_e\omega_m(s)\right]\notag \end{align*}](https://stringblog.com/wp-content/ql-cache/quicklatex.com-2ee49543579042e3ba1610ac90df6e49_l3.png)
因为![]() 非常小,在前馈量中可以近似忽略,这样式(4)可以整理为
非常小,在前馈量中可以近似忽略,这样式(4)可以整理为
(5) 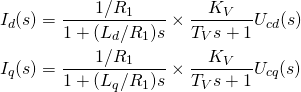
此时系统的![]() 、
、![]() 轴已经完全解耦。
轴已经完全解耦。
参考文献:
[25] GRZESIAK L M, TARCZEWSKI T. PMSM servo-drive control system with a state feedback and a load torque feedforward compensation[J]. COMPEL – The international journal for computation and mathematics in electrical and electronic engineering, 2012, 32(1) : 364 – 382.
[26] 田逸, 张茂青, LIPO T A. 基于MATLAB 的交流永磁同步电机解耦控制研究[J]. 电气传动自动化, 2009, 31(3) : 15 – 18.