本文是本科毕业论文系列的第二篇,其他各篇请见《本科毕设:交流伺服系统控制环路问题研究》
本节将介绍基础的永磁同步伺服控制方法,构建电流环、速度环和位置环的控制框图。
根据上文《永磁同步电机的数学模型》可以得到永磁同步电机的在![]() –
–![]() 坐标系下的电压方程
坐标系下的电压方程
(1) ![]()
(2) ![]()
(3) ![]()
电流环
电流环控制对象是PWM逆变器、电动机电枢回路、电流采样和滤波电路[18, §5.6.1]。
PWM逆变器方面,如果忽略电子电路延时,仅考虑主电路逆变器的延时,逆变器可以看做一个一阶惯性环节。假设逆变器的工作频率为![]() ,其开关周期为
,其开关周期为![]() ,而装置延时时间
,而装置延时时间![]() 。对于一个数字控制器,如果在一个逆变器周期内采样两次,可以得到装置近似延迟时间为
。对于一个数字控制器,如果在一个逆变器周期内采样两次,可以得到装置近似延迟时间为![]() ,由此可以得到逆变器环节的传递函数为
,由此可以得到逆变器环节的传递函数为
(4) ![]()
其中![]() 为逆变器的放大倍数。将上述模型近似为一个一阶惯性环节得到
为逆变器的放大倍数。将上述模型近似为一个一阶惯性环节得到
(5) ![]()
电机模型方面,将式(1)拉普拉斯变换得到
(6) ![]()
(7) ![Rendered by QuickLaTeX.com \begin{align*} I_d(s)&=\frac{1/R_1}{1+(L_d/R_1)s}\left[U_d(s)+L_qI_q(s)\omega_r(s)\right]\\ I_q(s)&=\frac{1/R_1}{1+(L_q/R_1)s}\left[U_q(s)-L_dI_d(s)\omega_r(s)-\Psi_f\omega_r(s)\right] \end{align*}](https://stringblog.com/wp-content/ql-cache/quicklatex.com-ffbfbe0ef186f0c0629afdc026239e11_l3.png)
可以看出![]() 轴电流和
轴电流和![]() 轴电流相互耦合。在
轴电流相互耦合。在![]() 的控制策略下,
的控制策略下,![]() 轴电流十分小,因此
轴电流十分小,因此![]() ,所以式(7)可以近似为
,所以式(7)可以近似为
(8) ![]()
其中![]() 。由此即可实现近似解耦控制[16, §2.3.4]。
。由此即可实现近似解耦控制[16, §2.3.4]。
采样和滤波环节通常设计为一阶低通滤波器,它的时间常数为![]() [21, §4.2.2.1]。所以采样环节可以表示为
[21, §4.2.2.1]。所以采样环节可以表示为
(9) ![]()
之后我们可以得到![]() 轴和
轴和![]() 轴的控制框图如图1和图2所示。图中,
轴的控制框图如图1和图2所示。图中,![]() 和
和![]() 分别是
分别是![]() 轴和
轴和![]() 轴PI调节器的比例系数;
轴PI调节器的比例系数;![]() 和
和![]() 分别是
分别是![]() 轴和
轴和![]() 轴PI调节器的积分系数;
轴PI调节器的积分系数;![]() 和
和![]() 分别是
分别是![]() 轴和
轴和![]() 轴电流给定。从式(2)可以看出,对于表贴式同步电机
轴电流给定。从式(2)可以看出,对于表贴式同步电机![]() ,
,![]() 对于电机的转矩没有任何影响,所以控制中
对于电机的转矩没有任何影响,所以控制中![]() 一般取0。
一般取0。
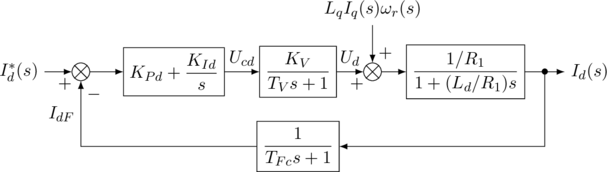
图1 ![]() 轴电流环控制框图
轴电流环控制框图
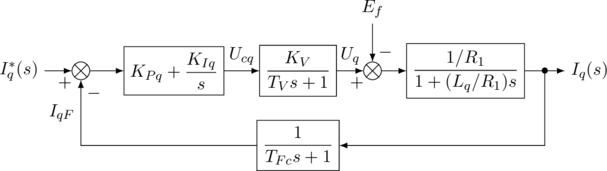
图2 ![]() 轴电流控制框图
轴电流控制框图
(10) 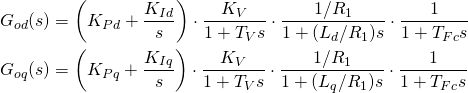
将逆变器引起的延时![]() 和滤波器引起的延时
和滤波器引起的延时![]() 两个小惯性环节近似叠加为一个延时[21, §4.2.2.1],取
两个小惯性环节近似叠加为一个延时[21, §4.2.2.1],取![]() ,则
,则
(11) 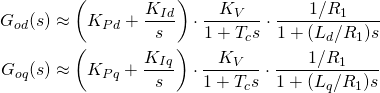
使PI调节器零点抵消控制对象中较大的时间常数极点,即由电机本身产生的极点[18, §5.6.1],取
(12) ![]()
(13) 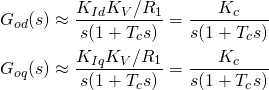
其中![]() 。电流环开环幅频响应如图3所示。
。电流环开环幅频响应如图3所示。
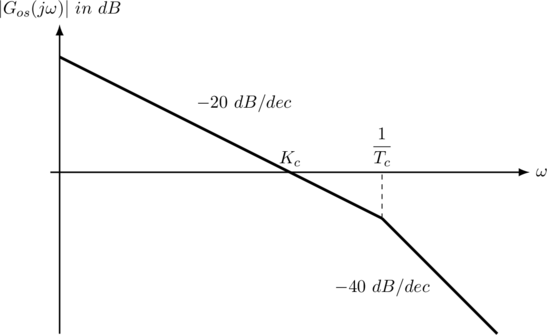
图3 电流环开环幅频响应
速度环
在速度环中,只需要考虑q轴电流,此时由式(13)可以得到![]() 轴电流环的闭环传函为
轴电流环的闭环传函为
(14) ![]()
因为![]() ,可以将该延时视为一个一阶小惯性环节,进而将闭环传函进一步简化为
,可以将该延时视为一个一阶小惯性环节,进而将闭环传函进一步简化为
(15) ![]()
式(15)即为速度环中电流环简化模型,进行近似需要满足如下条件[22, §2.4.2]
(16) ![]()
电磁转矩方面,对于表贴电机![]() ;对于凸极电机由于
;对于凸极电机由于![]() 轴电流很小,可以认为
轴电流很小,可以认为![]() 。现定义转矩常数
。现定义转矩常数![]() ,所以
,所以![]() 轴电流和电磁转矩之间的关系由式(2)近似为
轴电流和电磁转矩之间的关系由式(2)近似为
(17) ![]()
将式(3)进行拉普拉斯变化得到
(18) ![]()
(19) ![]()
电机摩擦系数![]() 比较小,通常可以忽略不计[18, §5.6.1]或者视作负载转矩的一部分[21, §4.3.4.1]。因此,式(19)可以简化为
比较小,通常可以忽略不计[18, §5.6.1]或者视作负载转矩的一部分[21, §4.3.4.1]。因此,式(19)可以简化为
(20) ![]()
(21) ![]()
使用PI调节器的速度环控制框图如图4所示。图中,![]() 和
和![]() 分别是速度环PI调节器的比例系数和积分系数;
分别是速度环PI调节器的比例系数和积分系数;![]() 为系统的转速给定。
为系统的转速给定。
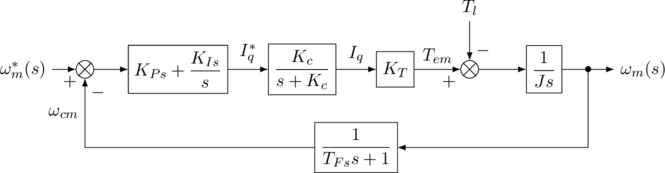
图4 使用PI调节器的速度环控制框图
(22) ![]()
将电流内环时间常数![]() 和滤波器引起的延时
和滤波器引起的延时![]() 两个小惯性环节近似叠加为一个延时[22, §2.4.2],取
两个小惯性环节近似叠加为一个延时[22, §2.4.2],取![]() ,则
,则
(23) 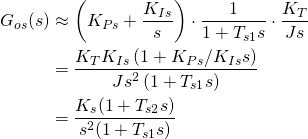
其中,![]() ;
;![]() 。
。
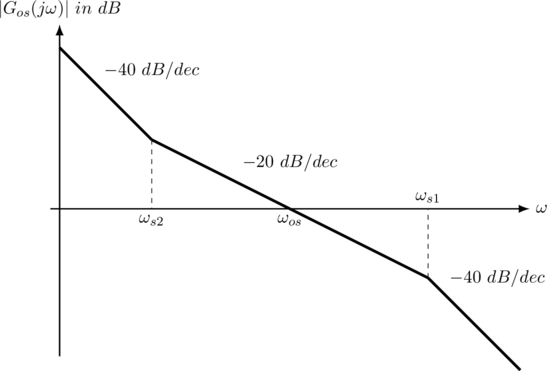
图5 使用PI调节器的速度环开环幅频响应
现定义![]() 、
、![]() 、
、![]() 为系统的截止频率,可以绘制开环传函式(23)的幅频响应如图5所示。图中,横轴为系统的频率,纵轴为开环增益。可以看出,系统由三部分组成该:低频部分以
为系统的截止频率,可以绘制开环传函式(23)的幅频响应如图5所示。图中,横轴为系统的频率,纵轴为开环增益。可以看出,系统由三部分组成该:低频部分以![]() 的速率下降,此时系统的传函可以近似为
的速率下降,此时系统的传函可以近似为
(24) ![]()
(25) ![]()
(26) ![]()
系统的截止频率由![]() 求出,应用中频段近似传函式(25),系统截止频率约为
求出,应用中频段近似传函式(25),系统截止频率约为
(27) ![]()
位置环
由速度环开环传函式(23)可以得到速度环闭环传函为
(28) ![]()
因为系统速度响应远比位置响应快,即位置环截止频率远低于速度环截止频率[18, §5.6.1],且考虑到位置环主要在转速调节器的带宽内调节[21, §4.4.1],可以将速度环近似为一个与原传函有相同截止频率的一阶惯性环节,此时系统的开环传函可以简化为式(25),闭环传函可以简化为
(29) ![]()
位置伺服系统不希望位置出现超调和振荡,以免位置控制精度下降,因此位置控制器应当采用比例调节器[18, §5.6.1]。因为位置环的测量通常使用码盘测量,无需在反馈测量回路进行滤波。
由此可以得到位置环控制框图如图6所示。图中,![]() 为比例调节器的比例系数;
为比例调节器的比例系数;![]() 和
和![]() 分别为系统的位置给定和位置输出。
分别为系统的位置给定和位置输出。

图6 位置环控制框图
(30) ![]()
(31) 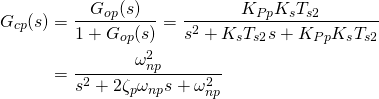
式中,![]() 为振荡角频率;
为振荡角频率;![]() 为阻尼系数。
为阻尼系数。
综合控制框图
由上文得到永磁同步伺服系统综合控制框图如图7所示。该框图不包含![]() 轴电流,
轴电流,![]() 轴电流的控制框图为图1。
轴电流的控制框图为图1。
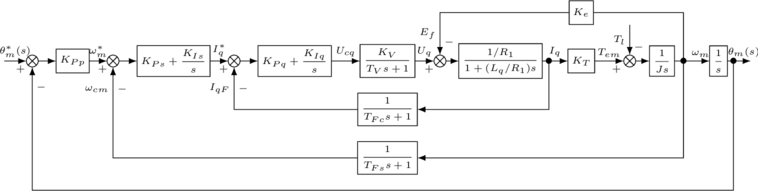
图7 永磁同步电机综合控制框图
图中,![]() 为系统的反电动势常数,当采用功率不变的Park变换和Clarke变换的情况下,
为系统的反电动势常数,当采用功率不变的Park变换和Clarke变换的情况下,![]() 和
和![]() 定义相同,所以在国际单位制(SI Unit)情况下(
定义相同,所以在国际单位制(SI Unit)情况下(![]() 的国际单位是
的国际单位是![]() ;
;![]() 的国际单位是
的国际单位是![]() ),两个常数值是相同的[24];当采用幅值不变的Park变换和Clarke变换的情况下,
),两个常数值是相同的[24];当采用幅值不变的Park变换和Clarke变换的情况下,![]() 。实际系统中需要考虑到功率因数、d轴电流等因素,两者并非完全遵循上述等式。
。实际系统中需要考虑到功率因数、d轴电流等因素,两者并非完全遵循上述等式。
总结
本文主要介绍了永磁同步电机的基本控制原理,其中电流环采用了近似解耦方式,实际控制中为达到更好的解耦效果,通常需要完全解耦,详见《永磁同步电机的完全解耦控制》。
参考文献:
[16] 王耕, 王晓雷. 控制电机及其应用(修订版)[M]. 北京: 电子工业出版社, 2012.
[18] 孙冠群, 李璟, 蔡慧. 控制电机与特种电机[M]. 第2 版. 北京: 清华大学出版社, 2016.
[21] SUL S-K. Control of Electric Machine Drive System[M]. Hoboken NJ: JOHN WILEY & SONS INC, 2011.
[22] 陈伯时. 电力拖动自动控制系统:运动控制系统[M]. 第3 版. 北京: 机械工业出版社, 2003.
[23] 彭瑞. 永磁同步电机交流伺服系统的研究[D]. 南京: 南京航空航天大学, 2007.
[24] The Northwestern University mechatronics design wiki. Mystery Motor Data Sheet[EB/OL]. 2011 [2017-04-19]. http://hades.mech.northwestern.edu/images/6/61/Asst7.pdf.