本文是本科毕业论文系列的第一篇,其他各篇请见《本科毕设:交流伺服系统控制环路问题研究》
本节将重点针对表贴式永磁同步电机,分析其稳态模型,并分析电机在ABC坐标系、![]() –
–![]() 坐标系和
坐标系和![]() –
–![]() 坐标系下数学模型。
坐标系下数学模型。
永磁同步电机的稳态性能
对于一般永磁同步电动机而言,根据双反应理论得到其电压方程为[17, §6.2]
(1) ![]()
其中,![]() 是电机外部施加的电压;
是电机外部施加的电压;![]() 为永磁气息基波磁场产生的反电动势;
为永磁气息基波磁场产生的反电动势;![]() 为电枢绕组中的电流,可以将其分解为直轴分量
为电枢绕组中的电流,可以将其分解为直轴分量![]() 和交轴分量
和交轴分量![]() ;
;
![]() 为电枢中的电阻,
为电枢中的电阻,![]() 为电枢中的电感;
为电枢中的电感;![]() 和
和![]() 分别为直轴和交轴中的电枢反应电抗。根据式(1)我们可以得到这样的向量图如图1所示。
分别为直轴和交轴中的电枢反应电抗。根据式(1)我们可以得到这样的向量图如图1所示。
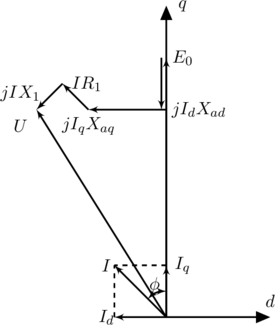
图1 永磁电动机模型向量图
在式(1)中的电流有如下关系
(2) ![]()
(3) ![]()
那么式(1)可以表示为
(4) ![]()
永磁同步电机的数学模型
为了便于对于永磁同步电机的数学模型进行分析,我们做出下面几个假设:
- 忽略电动机的铁芯饱和;
- 将电机中的磁滞损耗以及涡流损耗忽略不计;
- 定转子磁动势产生的磁场按照定子内部圆以正弦形式分布,即不考虑磁场中的除了基波外的其他高次谐波;
- 转子不设置阻尼绕组,永磁体也同样不带有阻尼作用;
- 各相绕组完全对称,即各相绕组的匝数相同、电阻相同、电感相同,各相轴线在电机中均匀分布,绕组轴线之间距离相同。
永磁同步电机的模型可以由两个部分组成,分别是机械模型和绕组电压模型。其中,机械模型与绕组电压使用的坐标系无关。电动机的机械运动方程为
(5) ![]()
式中,![]() 为电机的电磁转矩;
为电机的电磁转矩;![]() 为电动机负载转矩;
为电动机负载转矩;![]() 为电动机转子及负载转动惯量;
为电动机转子及负载转动惯量;![]() 为电动机粘滞摩擦系数;
为电动机粘滞摩擦系数;![]() 为电动机机械角速度。
为电动机机械角速度。
下面将基于上面的假设,分别建立各个坐标系下的永磁同步伺服电机模型。
静止坐标系(ABC)下的模型
如图2,永磁同步电机三相集中绕组分别为![]() 、
、![]() 、
、![]() ,
,![]() 是转子上永磁硅钢片的永磁磁场;
是转子上永磁硅钢片的永磁磁场;![]() 为电机的极对数;
为电机的极对数;![]() 是电机的电角速度;
是电机的电角速度;![]() 是转子磁场和
是转子磁场和![]() 相之间的夹角,显然
相之间的夹角,显然![]() 。
。
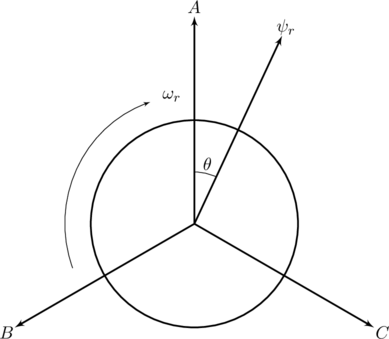
图2 永磁同步电机在ABC坐标系下的模型
(6) 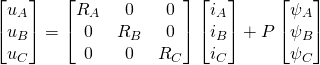
式中,![]() 、
、![]() 、
、![]() 是各相端电压;
是各相端电压;![]() 、
、![]() 、
、![]() 是各相定子相电阻;
是各相定子相电阻;![]() 、
、![]() 、
、![]() 是各相线电流;
是各相线电流;![]() 、
、![]() 、
、![]() 为各相总磁链;
为各相总磁链;![]() 为微分算子,即
为微分算子,即![]() 。
。
(7) 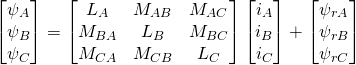
式中,![]() 为绕组自感;
为绕组自感;![]() 为绕组互感;
为绕组互感;![]() 为永磁磁链在各相中的交链,是
为永磁磁链在各相中的交链,是![]() 的函数。
的函数。
对于表贴式永磁同步电机,进一步作出下面假设:
- 电机气隙分布均匀,磁路与转子位置无关,既各绕组自感、绕组间互感与转子位置无关;
- 不考虑磁路的饱和,既自感和互感与通入绕组的电流大小无关,不考虑漏磁通带来的影响;
- 转子磁链呈正弦分布。
(8) 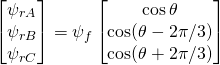
式中,![]() 是转子永磁体磁链的最大值,对某一永磁电机而言是常数。
是转子永磁体磁链的最大值,对某一永磁电机而言是常数。
因为三相绕组是空间对称的,通入的电流也是空间对称的,我们可以得到如下关系[18, §5.5.4]:
(9) 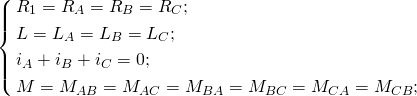
令![]() 由此可以将式(6)简化
由此可以将式(6)简化
(10) 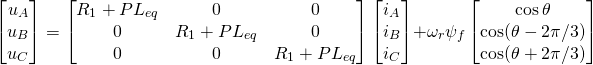
静止坐标系(α-β)下的数学模型
如图3,选取![]() 轴和
轴和![]() 轴重合,
轴重合,![]() 轴超前
轴超前![]() 轴
轴![]() ,
,![]() 、
、![]() 、
、![]() 分别为
分别为![]() 、
、![]() 、
、![]() 轴的绕组中的磁势;
轴的绕组中的磁势;![]() 、
、![]() 分别代表
分别代表![]() 、
、![]() 轴中的等效绕组磁势。
轴中的等效绕组磁势。
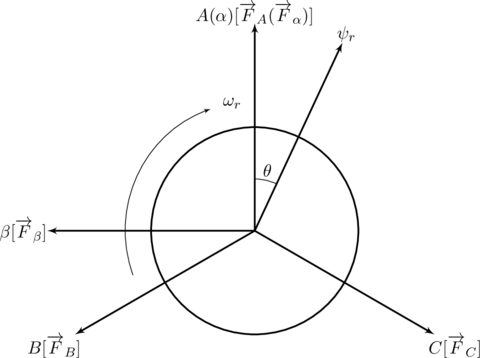
图3 永磁同步电机在![]() –
–![]() 坐标系下的模型
坐标系下的模型
由图3可以得到下面的等效关系
(11) 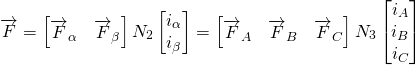
式中,![]() 为总磁势;
为总磁势;![]() 为两相
为两相![]() 、
、![]() 等效绕组匝数;
等效绕组匝数;![]() 为三相绕组
为三相绕组![]() 、
、![]() 、
、![]() 匝数。由式(11)得到电流之间的关系
匝数。由式(11)得到电流之间的关系
(12) 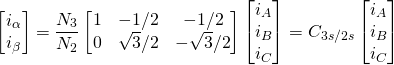
(13) ![]()
(14) ![]()
(15) 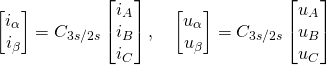
(16) ![]()
旋转坐标系下(d–q)的数学模型
如图4所示,构建永磁同步电机的![]() –
–![]() 坐标系。其中
坐标系。其中![]() 轴在转子磁极轴线上,
轴在转子磁极轴线上,![]() 轴超前于
轴超前于![]() 轴
轴![]() 电角度,
电角度,![]() –
–![]() 坐标系的旋转角速度即为永磁磁场的旋转的电角速度
坐标系的旋转角速度即为永磁磁场的旋转的电角速度![]() 。
。
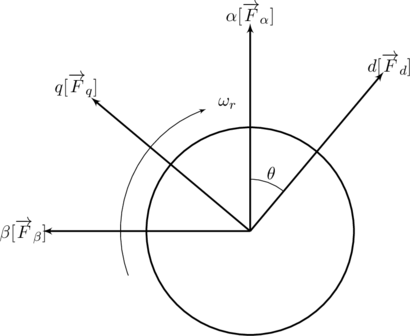
图4 永磁同步电机在![]() –
–![]() 坐标系下的模型
坐标系下的模型
(17) ![]()
式中,![]() 为
为![]() –
–![]() 轴上的集中绕组匝数,由此我们可以得到
轴上的集中绕组匝数,由此我们可以得到![]() –
–![]() 坐标系和
坐标系和![]() –
–![]() 坐标系中的电流转换关系
坐标系中的电流转换关系
(18) ![]()
(19) ![]()
(20) 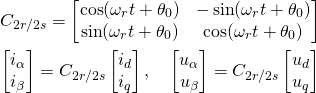
将上式带入式(16)中可以得到
(21) ![]()
其中,![]() 和
和![]() 分别为
分别为![]() 轴和
轴和![]() 轴的等效电阻,对于表贴式同步电机而言
轴的等效电阻,对于表贴式同步电机而言![]() 。如果初始状态下
。如果初始状态下![]() 轴和
轴和![]() 轴重合,上式进一步简化为
轴重合,上式进一步简化为
(22) ![]()
(23) ![]()
(24) ![]()
分别为![]() 轴和
轴和![]() 轴旋转电势。三相永磁同步伺服电动机的电磁功率定义为电磁转矩和电动机的转子角速度的乘积[16, §2.2.4],在幅值不变的变换条件下,电磁转矩表达式为
轴旋转电势。三相永磁同步伺服电动机的电磁功率定义为电磁转矩和电动机的转子角速度的乘积[16, §2.2.4],在幅值不变的变换条件下,电磁转矩表达式为
(25) ![Rendered by QuickLaTeX.com \begin{equation*} \begin{split} T_{em}&=\frac{3}{2}\frac{P_{em}}{\omega_m} =\frac{3}{2}\cdot p\cdot\frac{e_di_d+e_qi_q}{\omega_r}\\ &=\frac{3}{2}\cdot p\cdot\left[\Psi_fi_q+(L_d-L_q)i_di_q\right] \end{split} \end{equation*}](https://stringblog.com/wp-content/ql-cache/quicklatex.com-99249ffb21806954e72de669dafaa715_l3.png)
因为采用幅值不变的变化,转矩变化后的比例系数为![]() [20]。
[20]。
总结
本文分析了 重点推理了永磁同步电机在ABC向象限下、![]() –
–![]() 象限下和
象限下和![]() –
–![]() 象限下的数学模型,通常为了方便控制,采用其
象限下的数学模型,通常为了方便控制,采用其![]() –
–![]() 模型研究控制原理,详见《永磁同步伺服的闭环控制方法》。
模型研究控制原理,详见《永磁同步伺服的闭环控制方法》。
参考文献:
[16] 王耕, 王晓雷. 控制电机及其应用(修订版)[M]. 北京: 电子工业出版社, 2012.
[17] 辜承林, 陈乔夫, 熊永前. 电机学[M]. 第三版. 武汉: 华中科技大学出版社, 2010.
[18] 孙冠群, 李璟, 蔡慧. 控制电机与特种电机[M]. 第2 版. 北京: 清华大学出版社, 2016.
[19] 马志源. 电力拖动控制系统[M]. 北京: 科学出版社, 2004: 203 – 216.
[20] PILLAY P, KRISHNAN R. Modeling of permanent magnet motor drives[J]. IEEE Transactions on Industrial Electronics, 1988, 35(4) : 537 – 541.
描述“其中,L_d和L_q分别为d轴和q轴的等效电阻”是不是不对,另外能否解释下 R1和Rs的关系?
L_d和L_q分别为d轴和q轴的等效电感,这个的R_s和R_1应该是同样的,即相电阻。
我有几年没有搞这方面内容了,建议您推导一下,我也不敢保证我的记忆是对的。
thanks
公式(10)最后面的那个矩阵是错的吧,或者缺一个对西塔的求导。
这部分应该是对的, 是
是 ,求导后多出来
,求导后多出来 ,这个
,这个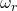 是电角速度
是电角速度
我不敢百分百确定,你可自己再推一遍
dq矩阵那里,永磁磁链应该在d分量上吧,你好像dq写反了(22及往下)
我感觉应该是没有错的,d和alpha重合的情况下theta为0,即sin(theta)=0, cos(theta)=1