空间矢量脉冲控制（SVPWM）

浩 Hao控制类，电力拖动

本文是本科毕业论文系列的第四篇，其他各篇请见《本科毕设：交流伺服系统控制环路问题研究》

本文将介绍空间适量脉冲控制SVPWM的基本原理，结合其他毕设文章以永磁同步电机为例。

空间矢量调制技术，即SVPWM（Space Vector Pulse Width Modulation）是一种较为新颖的PWM调制方法。早期的调制方法常采用正弦脉冲宽度调制，即SPWM（Sinusoidal Pulse Width Modulation），但SVPWM与之相比提高了电压的利用率，提升了同样直流侧电压的情况下输出最大电压[28]，而且能更好的抑制谐波畸变[27]，并易于通过数字算法实现[28]，故而更加广泛的应用于交流电机的控制中。

典型的三相逆变电路如图1所示。逆变电路中一共有6个开关管，三相电路每相各两个，显然每相电路上下两个桥臂不能同时导通，所以现在定义每相开关函数S_x (x=a, b, c)为

(1)   \begin{equation*} S_x=\begin{cases} 1&\text{Connect the upper switch}\\ 0&\text{Connect the lower switch} \end{cases} \end{equation*}

因此，在PWM调制过程中瞬时电压状态可以定义为[u_{aN}, u_{bN}, u_{cN}]^T=U_d\times[S_a, S_b, S_c]^T。其中，U_d为直流侧电压。

 

图1 使用IGBT的典型三相逆变电路

一般而言，对于m相系统中的某一物理量（如：电压、电流、磁链）的m个变量x_1、x_2…x_m，其大小可以视作\bm{x_1}、\bm{x_2}…\bm{x_m}的模，其空间位置（方向）位于各自绕组的轴上，之后将这些矢量相加并乘以2/m所得的合成矢量即为该物理量的综合矢量。[19, ξ10.2.2]

所以，对于三相永磁同步系统，可以定义其综合空间电压矢量

(2)   \begin{equation*} \bm{u}=\frac{2}{3}(u_a\bm{a}+u_b\bm{b}+u_c\bm{c}) \end{equation*}

其中，\bm{a}、\bm{b}和\bm{c}分别为矢量(1,0)、(1,2\pi/3)和(1,-2\pi/3)（极坐标系下）。在不进行PWM调制的情况下，显然，S_a、S_b和S_c相互组合只有2^3=8种不同的状态，所以\bm{u}也只有8种不同的取值。现分别将这8个空间矢量标注如图2所示。将八个矢量括号中的数字视作二进制，则亦可以得到十进制标注的八个矢量\bm{u_0}、\bm{u_1}…\bm{u_8}。

Rendered by QuickLaTeX.com

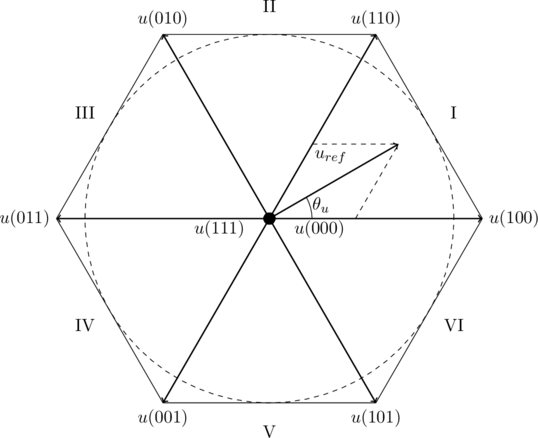
图2  8个基本空间矢量

从图2可以看出，八个矢量中\bm{u_1}、\bm{u_2}、\bm{u_3}、\bm{u_4}、\bm{u_5}、\bm{u_6}和\bm{u_7}的模都为(2/3)U_d，而\bm{u_0}和\bm{u_8}的模都为0。这八个矢量将空间分为6个扇区，即为图中I至VI。

从图2还可以看出，其他任意电压向量都可以变为\bm{u_1}至\bm{u_7}中两个向量的和，虽然本身系统只能输出这个八个电压，但经过PWM调制，系统实际上可以输出电压矢量图六棱形区域中任意的电压矢量。现以图中的\bm{u_{ref}}为例，\bm{u_{ref}}在第I扇区，与\bm{u_4}的夹角为\theta_u，这样可以将\bm{u_{ref}}向\bm{u_4}和\bm{u_6}分解为两个分量\bm{u_{ref4}}和\bm{u_{ref6}}，即

(3)   \begin{equation*} \bm{u_{ref}}=\bm{u_{ref4}}+\bm{u_{ref6}} \end{equation*}

而\bm{u_{ref4}}和\bm{u_{ref6}}两个向量可以通过\bm{u_4}和\bm{u_6}两个向量经过PWM调制获得。现假设PWM波的周期为T，在一个PWM周期内，\bm{u_4}导通的时间T_4，\bm{u_6}导通的时间为T_6，\bm{u_0}（或\bm{u_7}）导通的时间为T_0（或T_7），那么

(4)   \begin{gather*} T=T_4+T_6+T_0\\ \bm{u_{ref}}=\bm{u_{ref4}}+\bm{u_{ref6}}+0 =\frac{T_4}{T}\bm{u_4}+\frac{T_6}{T}\bm{u_6}+\frac{T_0}{T}\times 0 \label{eq:uref2} \end{gather*}

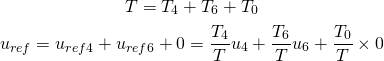
推广式(4)到任意向量得到

(5)   \begin{gather*} T=T_x+T_y+T_0\\ \bm{u_{ref}}=\frac{T_x}{T}\bm{u_x}+\frac{T_y}{T}\bm{u_y}+\frac{T_0}{T}\times 0 \label{eq:uref3} \end{gather*}

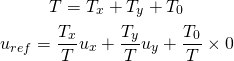
所以只需要控制三个向量在一个周期内存在时间就可以得到任意向量，只要控制对应的桥臂导通时间就可以获得任意三相电压。

由式(5)可以看出三个矢量采用任何的导通顺序都能产生相同的\bm{u_{ref}}向量，但为了取得更好的效果，三个空间矢量的安排应当满足下面的原则：

  • 每次矢量变化都只改变一个桥臂上的一组开关管；
  • 尽可能减少开关管切换次数，减少开关管开通关断过程中的损耗；
  • 力求减小系统谐波分量，尤其是低频信号的谐波分量；
  • 易于通过算法实现，尽可能减少计算时间；

有两种比较合适的方案满足上述条件，分别是对称调制模式和低开关损耗模式。

对称调制模式

图3为空间矢量和扇区和三相正弦电压波形之间的关系。现以I扇区为例，在I扇区中，恒有u_a>u_b>u_c，对于一个确定的电压向量\bm{u_{ref}}而言，有u_{refa}>u_{refb}>u_{refc}，其中u_{refa}、u_{refb}和u_{refc}分别是三相在\bm{u_{ref}}情况下的瞬时电压值。这样可以通过三角波对电压值进行如图4所示的取样，从图中可以直接读出开关函数S_x的取值。

Rendered by QuickLaTeX.com

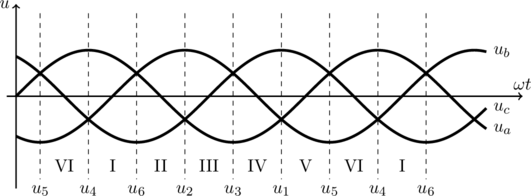
图3  空间矢量和扇区与三相正弦电压波形之间的关系

Rendered by QuickLaTeX.com

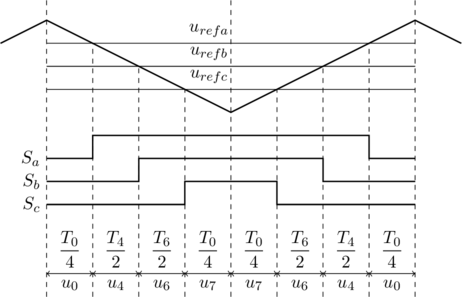
图4  采用对称调制模式的SVPWM调制方法

低开关损耗模式

若将图4中的\bm{u_7}变为\bm{u_0}并移动到两侧，可以得到图5所示的波形。此波形仍然满足式(5)，但此时C相两个开关状态都不需要发生改变，这明显减少了开关过程中的损耗，但与此同时带来了更多的谐波分量[19, §11.5.3]。

Rendered by QuickLaTeX.com

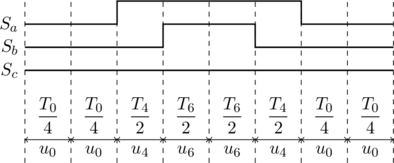
图5  采用低开关损耗模式的SVPWM调制方法

SVPWM输出向量如果超过图2中六棱形区域，会导致T_{x}+T_{y}>T，所以这是不可能实现的。当输出向量处于六棱形和圆形之间的区域时，电压矢量转动过程中会出现饱和的情况，这会导致输出波形变为平顶波，引入明显的低频奇次谐波分量。所以，一般控制电压向量处于圆形区域内，即输出的最大电压向量的模不超过\frac{\sqrt{3}}{2}|\bm{u}|，逆变器输出最大相电压峰值不超过\frac{\sqrt{3}}{2}\times\frac{2}{3}U_d=\frac{\sqrt{3}}{3}U_d。当采用SPWM时，逆变器所能输出的最大相电压仅为\frac{1}{2}U_d[19, §11.5.4]，低于SVPWM输出幅值，这也意味着SVPWM的直流电压利用率更高。

参考文献：

[19] 马志源. 电力拖动控制系统[M]. 北京: 科学出版社, 2004 : 203 – 216.

[27] KUMAR K V, MICHAEL P A, JOHN J P S S, et al. Simulation and comparison of SPWM and SVPWM control for three phase inverter[J]. Journal of Engineering & Applied Sciences, 2010, 5(7).

[28] 赵辉, 胡仁杰. SVPWM 的基本原理与应用仿真[J]. 电工技术学报, 2015, 30(14) : 350 – 353.

发表评论